Lũy thừa là một phép toán toán học, được viết dưới dạng aⁿ, bao gồm hai số, cơ số a và số mũ hoặc lũy thừa n, và được phát âm là “a lũy thừa n”. Khi n là một số nguyên dương, lũy thừa tương ứng với phép nhân lặp của cơ số: nghĩa là aⁿ là tích của phép nhân n cơ số. Bài viết hôm nay, VerbaLearn sẽ trình bày đến bạn đọc chi tiết công thức lũy thừa và một số dạng bài tập vận dụng theo chương trình toán 12.
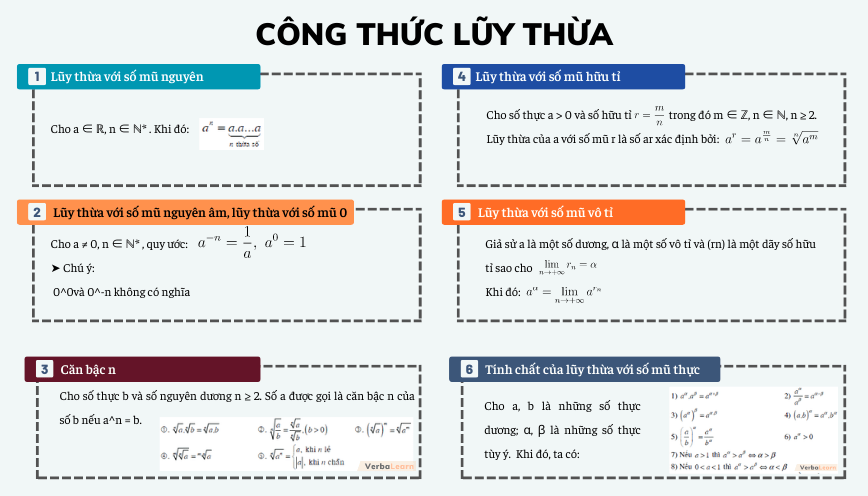
Công thức lũy thừa
1. Lũy thừa với số mũ nguyên
Cho a ∈ ℝ, n ∈ ℕ* . Khi đó: ![]()
2. Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
Cho a ≠ 0, n ∈ ℕ* , quy ước:
Chú ý:
00 và 0-n không có nghĩa
Người ta thường dùng các lũy thừa của 10 với số mũ nguyên để biểu thị những số rất lớn và những số rất bé. Chẳng hạn: Khối lượng của Trái Đất là 5,97.1024 kg; khối lượng nguyên tử của hiđrô là 1,66.10-24 kg .
3. Căn bậc n
Cho số thực b và số nguyên dương n ≥ 2. Số a được gọi là căn bậc n của số b nếu an = b
Khi n lẻ và b ∈ ℝ
Tồn tại duy nhất căn bậc n của b , kí hiệu
Khi n chẵn
b < 0: Không tồn tại căn bậc n của b
b = 0: Có một căn bậc n của b , kí hiệu
b > 0: Có hai căn bậc n của b trái dấu, kí hiệu giá trị dương là , còn giá trị âm là
Tính chất của căn bậc n
Với hai số không âm a, b; hai số nguyên dương m, n ta có:
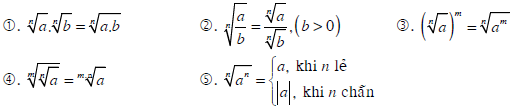
4. Lũy thừa với số mũ hữu tỉ
Cho số thực a > 0 và số hữu tỉ , trong đó m ∈ ℤ, n ∈ ℕ, n ≥ 2.
Lũy thừa của a với số mũ r là số ar xác định bởi:
5. Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, α là một số vô tỉ và (rn) là một dãy số hữu tỉ sao cho
Khi đó:
6. Tính chất của lũy thừa với số mũ thực
Cho a, b là những số thực dương; α, β là những số thực tùy ý. Khi đó, ta có:
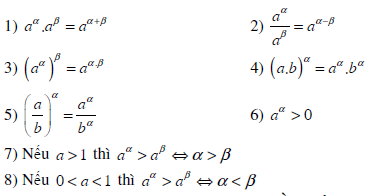
Phân dạng bài tập
Dạng 1. Tính các giá trị của một biểu thức – Rút gọn biểu thức.
Bài tập vận dụng
Câu 1. Tính các biểu thức sau
Hướng dẫn giải
Câu 2. Tính các biểu thức sau
Hướng dẫn giải
Câu 3. Tính các biểu thức sau:
Hướng dẫn giải
Câu 4. Tính các biểu thức sau
Hướng dẫn giải
Câu 5. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Câu 6. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Câu 7. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Dạng 2. Chứng minh đẳng thức, bất đẳng thức – So sánh giá trị của biểu thức
Phương pháp giải
Ta cần chú ý một số điều sau:
– Nếu a > 1 thì α < β ⇔ aα < aβ
– Nếu 0 < a < 1 thì α < β ⇔ aα > aβ
Bài tập vận dụng
Câu 1. Hãy so sánh các cặp số sau
Hướng dẫn giải
a) Ta có
Do 12 < 18 nên
Vì cơ số a = 5 > 1 nên
b) Ta có
c) Ta có
d) Ta có
Câu 2. Hãy so sánh các cặp số sau
Hướng dẫn giải
a) Đưa hai căn đã cho về cùng căn bậc 15, ta được:
Do 100000 > 8000 nên
b) Ta có
Do 125 < 2401 nên
c) Ta có
Do 371293 > 279841 nên
d) Ta có
Câu 3. Hãy so sánh các cặp số sau
Hướng dẫn giải
a) Ta có
Do 8 < 9 nên
b) Ta có
c) Ta có
d) Ta có
Câu 4. Không dùng máy tính và bảng số. Chứng minh:
Hướng dẫn giải
a)
Cách 1. Ta có: .
Tương tự:
Suy ra:
Cách 2. Đặt . Ta cần chứng minh x = 2
Ta có:
Từ đó ta có: x3 + 3x – 14 = 0 ⇔ (x – 2)(x2 + 2x + 7) = 0 ⇔ x = 2 (vì x2 + 2x +7 > 0)
Cách 3. Ta có: . Do đó
nếu
và
là nghiệm của phương trình X2 – 2X – 1 = 0, tức là:
Ta chứng minh đẳng thức (1). Ta có: . Từ đó suy ra (1).
Đẳng thức (2) chứng minh tương tự. Từ (1) và (2) suy ra điều phải chứng minh.
b)
Đặt . Ta cần chứng minh x = 3
Ta có:
⇔ x3 – 5x – 12 = 0 ⇔ (x – 3)(x2 + 3x + 4) = 0 ⇔ x = 3 (vì x2 + 3x + 4 > 0)
c)
Cách 1. Ta có:
Vì nên
Cách 2. Ta có:
Nên
d)
Có thể giải bằng ba cách như câu a)
Đặt H68. Ta cần chứng minh x = 3
Ta có: ⇔ x3 – 3x – 18 = 0
⇔ (x – 3)(x2 + 3x + 6) = 0 ⇔ x = 3 (vì x2 + 3x + 6 > 0)
Bài tập tổng hợp
Câu 1. Hãy tính
Đáp án
Câu 2. Đơn giản các biểu thức sau
Đáp án
Câu 3. Đơn giản các biểu thức sau:
Đáp án
Câu 4. Đơn giản các biểu thức sau
Đáp án
Câu 5. So sánh các số:
Đáp án
Câu 6. Chứng minh rằng:
Câu 7. Rút gọn các biểu thức sau
Đáp án
Tài liệu tham khảo
Tài Liệu: Chuyên đề lũy thừa, mũ và lôgarit ôn thi THPTQG – Thầy Nguyễn Bảo Vương – 583 trang
Tài Liệu: Chuyên đề Mũ và Logarit – Thầy Đặng Việt Đông – 506 trang
Tài Liệu: Chuyên đề hàm số lũy thừa, hàm số mũ và hàm số logarit – Thầy Nguyễn Trọng – 99 trang
Tài Liệu: Chuyên đề hàm số lũy thừa, hàm số mũ và hàm số logarit – Thầy Lê Hồ Quang Minh – 173 trang
Tài Liệu: Tuyển tập các bài toán mũ và logarit hay và đặc sắc – Thầy Nguyễn Xuân Nhật – 88 trang
Tài Liệu: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit – Thầy Nguyễn Tài Chung – 96 trang
Tài Liệu: Phương pháp giải toán cực trị mũ – logarit – Tạp chí & Tư liệu toán học – 229 trang
Tài Liệu: Chuyên đề lũy thừa, mũ và logarit – Thầy Lư Sĩ Pháp – 179 trang
Tài Liệu: Chuyên đề lũy thừa, mũ và logarit – Thầy Bùi Trần Duy Tuấn – 341 trang
Tài Liệu: Các dạng bài tập VDC bất phương trình mũ và bất phương trình lôgarit – 27 trang
Tài Liệu: Chuyên đề phương trình mũ và logarit – Thầy Nguyễn Thành Long – 179 trang