Tính chất Môđun số phức
Mô đun của số phức: Số phức z = a + bi được biểu diễn bởi điểm M (a; b) trên mặt phẳng Oxy. Độ dài của vec tơ 
được gọi là mô đun của số phức z. Kí hiệu: 
Tính chất
Chú ý: 
Lưu ý:
|z1 + z2| ≤ |z1| + |z2| dấu bằng xảy ra ⇔ z1 = kz2 (k ≥ 0).
|z1 – z2| ≤ |z1| + |z2| dấu bằng xảy ra ⇔ z1 = kz2 (k ≤ 0).
|z1 + z2| ≥ ||z1| – |z2|| dấu bằng xảy ra ⇔ z1 = kz2 (k ≤ 0).
|z1 – z2| ≥ ||z1| – |z2|| dấu bằng xảy ra ⇔ z1 = kz2 (k ≥ 0).
|z1 + z2|2 + |z1 – z2|2 = 2 (|z1|2 + |z2|2)
Một số quỹ tích nên nhớ
Một số dạng toán thường gặp
Dạng 1: Quỹ tích điểm biểu diễn số phức là đường thẳng.
TQ1: Cho số phức z thỏa mãn |z – a – bi| = |z|, tìm |z|Min. Khi đó ta có
Quỹ tích điểm M (x; y) biểu diễn số phức z là đường trung trực đoạn OA với A (a; b)
TQ2: Cho số phức thỏa mãn điều kiện |z – a – bi| = |z – c – di|. Tìm |z|min. Ta có
Quỹ tích điểm M (x; y) biểu diễn số phức z là đường trung trực đoạn AB với A (a; b), B (c; d)
Lưu ý: Đề bài có thể suy biến bài toán thành 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về dạng cơ bản.
Ví dụ 1:
Cho số phức thỏa mãn điều kiện 
. Khi đó ta biến đổi
Cho số phức thỏa mãn điều kiện |iz – a – bi| = |z – c – di|. Khi đó ta biến đổi
Dạng 2: Quỹ tích điểm biểu diễn số phức là đường tròn.
TQ: Cho số phức z thỏa mãn điều kiện |z – a – bi| = R > 0 (|z – z0| = R). Tìm |z|Max, |z|Min. Ta có
Quỹ tích điểm M (x; y) biểu diễn số phức z là đường tròn tâm I (a; b) bán kính R
Lưu ý: Đề bài có thể ở dạng khác, ta cần thực hiện các phép biến đổi đưa về dạng cơ bản.
Ví dụ 1: Cho số phức z thỏa mãn điều kiện 
(Chia hai vế cho |i|)
⇔ |a + b + ai| = R
Ví dụ 2: Cho số phức z thỏa mãn điều kiện 
(Lấy liên hợp 2 vế)
Ví dụ 3: Cho số phức z thỏa mãn điều kiện
Hay viết gọn 
(Chia cả hai vế cho |z0|)
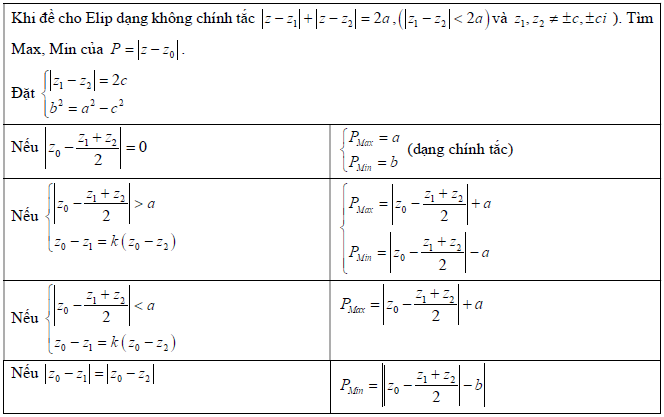
Dạng 3: Quỹ tích điểm biểu diễn số phức là Elip.
TQ1: (Elip chính tắc). Cho số phức z thỏa mãn điều kiện |z – c| + |z + c| = 2a, (a > c). Khi đó ta có
Quỹ tích điểm M (x; y) biểu diễn số phức z là Elip: 
TQ2: (Elip không chính tắc). Cho số phức z thỏa mãn điều kiện |z – z1| + |z – z2| = 2a
Thỏa mãn 2a > |z1 – z2|.
Khi đó ta thực hiện phép biến đổi để đưa Elip về dạng chính tắc
Ta có
Bài tập áp dụng
Câu 1: Cho số phức z thỏa mãn |z – 2 – 3i| = 1. Tìm giá trị lớn nhất của 
.
A. 
B. 
C. 
D. 
Lời giải
Chọn C.
Ta có 
Đặt 
, khi đó ⇔ |w – 3 + 2i| = 1
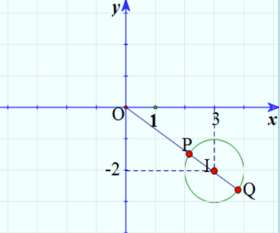
Tập hợp các điểm biểu diễn số phức là đường tròn (I; 1) và |w| là khoảng cách từ gốc tọa độ đến 1 điểm trên đường tròn. Do đó giá trị lớn nhất của |w| chính là đoạn OQ 
.
Nhận xét: Ở đây ta sử dụng kiến thức sau: 
Câu 2: Cho số phức z thỏa mãn |z – 6| + |z + 6| = 20. Gọi M, n lần lượt là mô đun lớn nhất và nhỏ nhất của z. Tính M – n
A. M – n = 2
B. M – n = 4
C. M – n = 7
D. M – n = 14
Lời giải
Gọi z = x + yi, (x, y ∊ ℝ). Theo giả thiết, ta có |z – 6| + |z + 6| = 20.
Gọi M (x; y), F1 (6; 0) và F2 (–6; 0).
Khi đó (*) ⇔ MF1 +MF2 = 20 > F1F2 = 12 nên tập hợp các điểm E là đường elip (E) có hai tiêu điểm F1 và F2. Và độ dài trục lớn bằng 20.
Ta có c = 6; 2a = 20 ⇔ a = 10 và b2 = a2 – c2 = 64 ⇒ b = 8.
Do đó, phương trình chính tắc của (E) là 
.
Suy ra max |z| = OA = OA’ = 10 khi z = ± 10 và min |z| = OB = OB’ = 8 khi z = ±8i.
Vậy M – n = 2.
Nhận xét: Ở trên ta đã sử dụng định nghĩa (E) để nhận dạng được phương trình elip
Câu 3: Xét số phức z = a + bi (a, b ∊ ℝ) thỏa mãn 
. Tính P = a + b khi |z + 1 – 3i| + |z – 1 + i| đạt giá trị lớn nhất.
A. P = 8
B. P = 10
C. P = 4
D. P = 6
Lời giải
Chọn B.
Gọi M (a; b) là điểm biểu diễn của số phức z.
Theo giả thiết ta có: 
⇒ Tập hợp điểm biểu diễn số phức z là đường tròn tâm I (4; 3) bán kính 
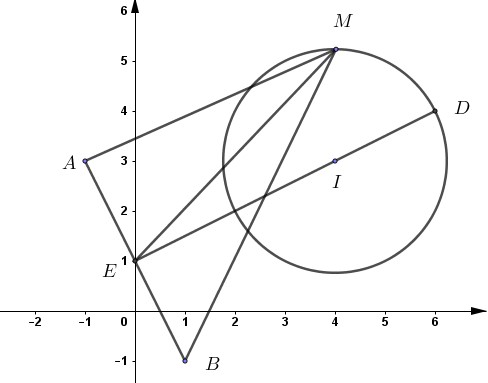
Gọi 
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D
Ta có: Q2 = MA2 + MB2 + 2MA.MB
⇔ Q2 ≤ MA2 + MB2 + MA2 + MB2 = 2 (MA2 + MB2)
Vì ME là trung tuyến trong ∆MAB
Mặt khác 
Cách 2: Đặt z = a + bi. Theo giả thiết ta có: (a – 4)2 + (b – 5)2 = 5.
Đặt 
. Khi đó:
Áp dụng BĐT Bunhiacopxki ta có:
Dấu bằng xảy ra khi 
.
Câu 4: Xét số phức z thỏa mãn thỏa mãn 
. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z – 1 + i|. Tính P = m + M.
A. 
B. 
C. 
D. 
Lời giải
Chọn A.
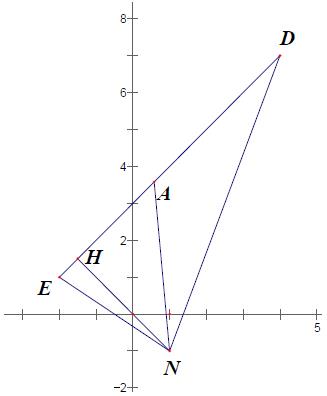
Gọi A là điểm biểu diễn số phức z, E (–2; 1), F (4; 7) và N (1; –1).
Từ AE + AF = và 
nên ta có A thuộc đoạn thẳng EF.
Gọi H là hình chiếu của N lên EF, ta có 
. Suy ra P = NH + NF ⇒ .
Câu 5: Cho số phức z thỏa mãn |z – 2 – 2i| = 1. Số phức z – i có mô đun nhỏ nhất là:
A. 
B. 
C. 
D. 
Lời giải
Chọn B.
Cách 1:
Đặt w = z – i ⇒ z = w + i.
Gọi M (x; y) là điểm biểu diễn hình học của số phức w.
Từ giả thiết |z – 2 – 2i| = 1 ta được:
|w + i – 2 – 2i| = 1 ⇔ |w – 2 – i| = 1 ⇔ | (x – 2) + (y – 1) i| = 1 ⇔ (x – 2)2 + (y – 1)2 = 1.
Suy ra tập hợp những điểm M (x; y) biểu diễn cho số phức w là đường tròn (C) có tâm I (2; 1) bán kính R = 1.
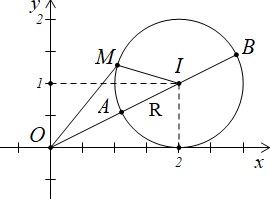
Giả sử OI cắt đường tròn (C) tại hai điểm A, B với A nằm trong đoạn thẳng OI.
Ta có |w| = OM
Mà OM + MI ≥ OI ⇔ OM + MI ≥ OA + AI ⇔ OM ≥ OA
Nên |w| nhỏ nhất bằng 
.
Cách 2:
Từ |z – 2 – 2i| = 1 ⇒ (a – 2)2 + (b – 2)2 = 1 với z = a + bi (a, b ∊ ℝ)
a – 2 = sinx; b – 2 = cosx ⇒ a = 2 + sinx, b = 2 + cosx
Khi đó: 
Nên |z – i| nhỏ nhất 
khi 
Ta được 
Cách 3:
Sử dụng bất đẳng thức ||z1| – |z2|| ≤ |z1 + z2| ≤ |z1| + |z2|
Câu 6: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 
với z là số phức khác 0 và thỏa mãn |z| ≥ 2. Tính tỉ số 
.
A. 
B. 
C. 
D. 
Lời giải
Chọn C.
Ta có 
Vậy
Câu 7: Xét tất cả các số phức z thỏa mãn |z – 3i + 4| = 1. Giá trị nhỏ nhất của |z2 + 7 – 24i| nằm trong khoảng nào?
A. (0; 1009)
B. (1009; 2018)
C. (2018; 4036)
D. (4036; +∞)
Lời giải
Chọn B.
Ta có 1 = |z – 3i + 4| ≥ ||z| – |3i – 4|| = ||z| – 5| ⇒ –1 ≤ |z| ≤ –5 ⇒ 4 ≤ z ≤ 6.
Đặt z0 = 4 – 3i ⇒ |z0| = 5; z02 = 7 – 24i.
Ta có 
Mà 
Suy ra 
Hàm số xảy ra khi và chỉ khi 
Do đó |z2 + 7 – 24i| nằm trong khoảng (1009; 2018).
Câu 8: Cho số phức z thỏa mãn 
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = |z – 2 – 2i|. Đặt A = M + m. Mệnh đề nào sau đây đúng?
A. 
B. 
C. 
D. 
Lời giải
Chọn A.
Giá sử: z = x + yi, (x, y ∊ ℝ) ⇒ N (x; y): điểm biểu diễn của số phức z trên mặt phẳng tọa độ Oxy.
Ta có
⇒ |x| + |y| = 2 ⇒ N thuộc các cạnh của hình vuông BCDF (hình vẽ).
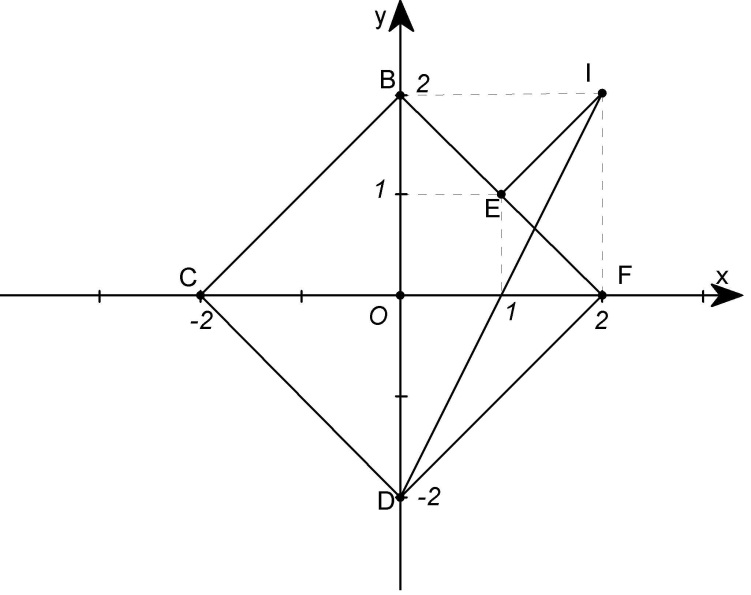
với I (2; 2)
Từ hình ta có: E (1; 1)
và 
Vậy 
.
Câu 9: Cho số phức z thỏa mãn |z – 3 + 4i| = 2 và w = 2z + 1 – i. Khi đó |w| có giá trị lớn nhất bằng
A. 
B. 
C. 
D. 
Lời giải
Chọn C.
Theo bất đẳng thức tam giác ta có
Vậy giá trị lớn nhất của |w| là .
Câu 10: Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức z (4 + 3i) và số phức liên hợp của nó có điểm biểu diễn là N và N’. Biết rằng M, M’, N, N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của |z + 4i – 5|.
A. 
B. 
C. 
D. 
Lời giải
Chọn C.
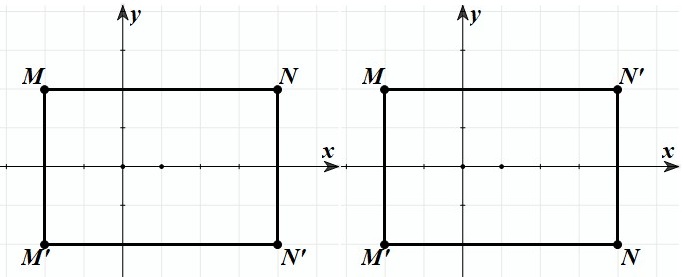
Gọi z = x + yi, trong đó x, y ∊ ℝ. Khi đó 
, M (x; y), M’ (x; –y).
Ta đặt w = z (4 + 3i) = (x + yi) (4 + 3i) = (4x – 3y) + (3x + 4y) i ⇒ N (4x – 3y; 3x + 4y). Khi đó:
Ta có M và M’; N và N’ từng cặp đối xứng nhau qua trục Ox. Do đó, để chúng tạo thành một hình chữ nhật thì yM = yN hoặc yM = yN’. Suy ra y = 3x + 4y hoặc y = –3x – 4y. Vậy tập hợp các điểm M là hai đường thẳng d1: x + y = 0 và d2: 3x + 5y = 0.
Đặt 
. Ta có P = MA với A (5; –4).
Pmin ⇔ MAmin ⇔ MA = d (A; d1) hoặc MA = d (A; d2). Mà 
.
Vậy Pmin = d (A; d1) =
Câu 11: Biết số phức z thỏa mãn |iz – 3| = |z – 2 – i| và |z| có giá trị nhỏ nhất. Phần thực của số phức z bằng
A. 
B. 
C. 
D. 
Lời giải
Chọn D.
Đặt z = x + yi (x, y ∊ ℝ).
Khi đó 
Lại có 
Thay (1) vào (2) ta được:
Dấu đẳng thức xảy ra khi 
Thay 
vào (1) suy ra 
Vậy phần thực của số phức z là .
Câu 12: Xét các số phức z thỏa mãn |z – 1 – 3i| = 2. Số phức z mà |z – 1| nhỏ nhất là
A. z = 1 + 5i
B. z = 1 + i
C. z = 1 + 3i
D. z = 1 – i
Lời giải
Chọn D.
Gọi z = x + yi (x, y ∊ ℝ). Khi đó M (x; y) là điểm biểu diễn của số phức z.
Theo bài ra ta có |z – 1 – 3i| = 2 ⇔ (x – 1)2 + (y – 3)2 = 4.
Suy ra tập hợp điểm M là đường tròn tâm I (1; 3) bán kính R = 2.
Khi đó 
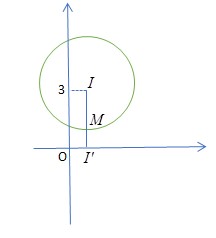
|z – 1| nhỏ nhất khi I’M ngắn nhất hay I, M, I’ thẳng hàng, M nằm giữa I và I’.
Phương trình đường thẳng II’ là x = 1.
Tọa độ giao điểm của đường thẳng II’ với đường tròn tâm I bán kính R = 2 là M1 (1; 1) và M1 (1; 5).
Thử lại ta thấy M1 (1; 1) thỏa mãn. Vậy z = 1 + i.
Câu 13: Cho số phức z thỏa mãn 
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = |z – 2 – 2i|. Đặt A = M + m. Mệnh đề nào sau đây đúng?
A. 
B. 
C. 
D. 
Lời giải
Chọn A.
Đặt z = x + yi và gọi M (x; y) là điểm biểu diễn của z = x + iy
Ta có ⇔ |x| + |y| = 2
Gọi A (2; 2) và P = MA
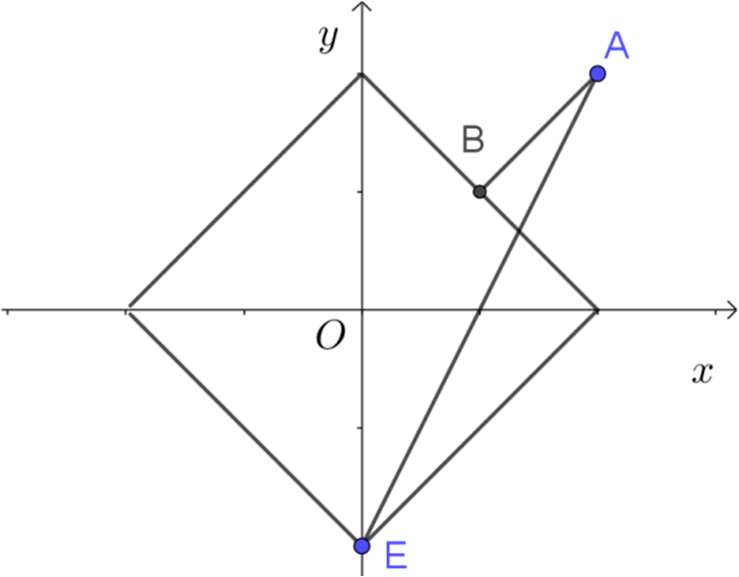
Theo hình vẽ, min P = d (A, ∆), với ∆: x + y = 2 và 
, với E (0; –2)
Vậy 
Câu 14: Trong các số phức z thỏa mãn 
, số phức z có mô đun nhỏ nhất có phần ảo là
A. 
B. 
C. 
D. 
Lời giải
Chọn D.
Gọi z = x + yi, (x, y ∊ ℝ) được biểu diễn bởi điểm M (x; y).
⇔ | (x – 1) + (y + 1) i| = | (x + 1) – (y + 2) i|
Cách 1:
Suy ra 
khi 
Vậy phần ảo của số phức z có mô đun nhỏ nhất là .
Cách 2:
Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn số phức z là đường thẳng d: 4x + 2y + 3 = 0.
Ta có |z| = OM. |z| nhỏ nhất ⇔ OM nhỏ nhất ⇔ M là hình chiếu của O trên d.
Tọa độ của M là nghiệm của hệ phương trình: 
Vậy phần ảo của số phức z có mô đun nhỏ nhất là .
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức z như sau:
Gọi M biểu diễn số phức z, điểm A (1; –1) biểu diễn số phức 1 – i, điểm B (–1; –2) biểu diễn số phức –1 – 2i.
Khi đó (*) ⇔ MA ≡ MB. Suy ra tập hợp điểm biểu diễn số phức z là đường trung trực của đoạn thẳng AB có phương trình d: 4x + 2y + 3 = 0.
Câu 15: Cho hai số phức z1, z2 thỏa mãn 
. Giá trị nhỏ nhất của |z1 – z2| là
A. 
B. 
C. 1
D. 
Lời giải
Chọn A.
Giả sử z1 = x1 + y1i với x1; y2 ∊ ℝ. Khi đó:
⇒ Quỹ tích điểm M biểu diễn số phức z1 là đường thẳng ∆: x – y + 3 = 0.
Giả sử z2 = x2 + y2i với x2; y2 ∊ ℝ. Ta có:
⇒ Quỹ tích điểm N biểu diễn số phức z2 là đường tròn (C): x2 + y2 – 4x + 2y + 3 = 0 có tâm I (2; –1) và bán kính 
.
Khoảng cách từ I đến ∆ là: 
⇒ đường thẳng ∆ và đường tròn C không có điểm chung.
Quỹ tích các điểm biểu diễn số phức z1 – z2 là đoạn thẳng MN. ⇒ |z1 – z2| nhỏ nhất khi và chỉ khi MN nhỏ nhất.
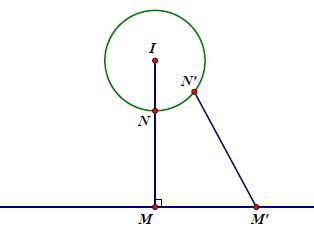
Dễ thấy 
.
Câu 16: Gọi S là tập hợp các số phức z thỏa mãn 
và |z + 1 + mi| = |z + m + 2i|, (trong đó m ∊ ℝ). Gọi z1, z2 là hai số phức thuộc S sao cho |z1 – z2| lớn nhất, khi đó giá trị của |z1 + z2| bằng
A. 2
B. 10
C. 
D. 
Lời giải
Chọn A.
Đặt z = x + yi, (x, y ∊ ℝ). Khi đó
⇔ (x – 1)2 + y2 = 34; |z + 1 + mi| = |z + m + 2i| ⇔ 2 (m – 1) x + 2 (2 – m) y + 3 = 0.
Do đó tập hợp các điểm M biểu diễn số phức z là giao điểm của đường tròn (C): (x – 1)2 + y2 = 34 và đường thẳng d: 2 (m – 1) x + 2 (2 – m) y + 3 = 0.
Gọi A, B là hai điểm biểu diễn z1 và z2. Suy ra (C) ∩ d = {A; B}.
Mặt khác 
do đó 
.
Từ đó ta có 
nên 
Vậy |z1 + z2| = 2.
Câu 17: Cho hai số phức z, w thỏa mãn 
. Biết rằng |z – w| đạt giá trị nhỏ nhất khi z = z0, w = w0. Tính |3z0 – w0|.
A. 
B. 
C. 1
D. 
Lời giải
Chọn D.
Ta có:
, suy ra tập hợp điểm biểu diễn M biểu diễn số phức z là đường tròn có tâm 
, bán kính 
.
, suy ra tập hợp điểm biểu diễn N biểu diễn số phức w là đường tròn có tâm 
, bán kính 
.
Ta có min |z – w| – min MN.
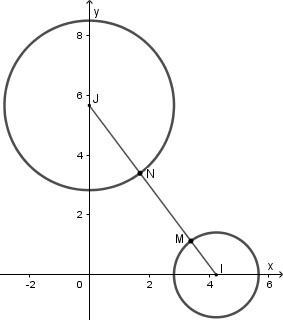
Mặt khác IM + MN + NJ ≥ IJ ⇒ MN ≥ IJ – IM – NJ hay 
.
Suy ra 
khi I, M, N, J thẳng hàng và M, N nằm giữa I, J (Hình vẽ).
Cách 1:
Khi đó ta có: 
và 
Mặt khác 
Suy ra 
Cách 2:
Ta có 
Do đó 
Cách 3:
Suy ra 
Câu 18: Cho hai số phức z và w thỏa mãn z + 2w = 8 – 6i và |z – w| = 4. Giá trị lớn nhất của biểu thức |z| + |w| bằng
A. 
B. 
C. 
D. 
Lời giải
Chọn C.
Giả sử M, N lần lượt là các điểm biểu diễn cho z và w. Suy ra 
, |z – w| = MN = 4 và Ò = 2OI = 10.
Đặt 
. Dựng hình bình hành OMFE
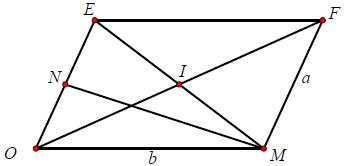
Ta có 
Suy ra 
, dấu “=” xảy ra khi 
Vậy (a + b) max =
Câu 19: Cho số phức z thỏa mãn |z| = |z + 1| + |z2 – z + 1|. Tính M.m
A. 
B. 
C. 
D. 
Lời giải
Chọn A.
Thay |z|2 = 1 vào P ta có
Mặt khác 
Đặt 
do |z| = 1 nên điều kiện t ∊ [–2; 2].
Suy ra 
Xét hàm số 
với t ∊ [–2; 2].
với t > 1. Suy ra f’ (t) > 0 với t > 1.
với t < 1. Suy ra 
Ta có bảng biến thiên
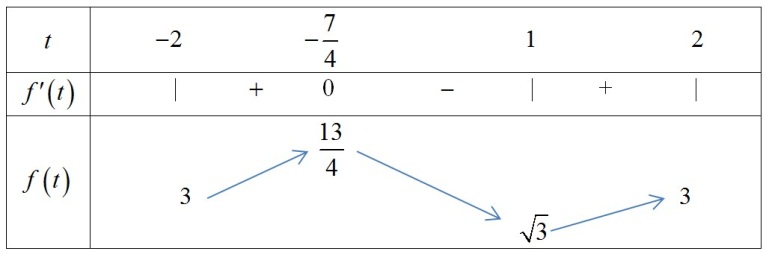
Từ bảng biến thiên suy ra 
tại 
và 
tại 
Vậy M. m =
Câu 20: Cho hai số phức z và ⍵ = a + bi thỏa mãn 
; 5a – 4b – 20 = 0. Giá trị nhỏ nhất của |z – ⍵| là
A. 
B. 
C. 
D. 
Lời giải
Chọn A.
Đặt 
, vì 
nên tập hợp các điểm M biểu diễn số phức z thuộc elip có 
Tập hợp các điểm N biểu diễn số phức ⍵ thuộc đường thẳng ∆: 5x – 4y – 20 = 0.
Yêu cầu bài toán trở thành tìm điểm M ∊ (E) và N ∊ ∆ sao cho MN nhỏ nhất.
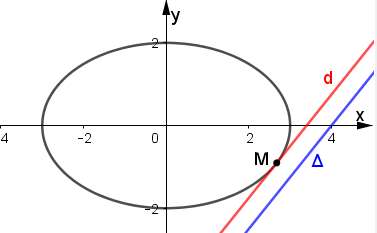
Đường thẳng d song song với ∆ có dạng d: 5x – 4y + c = 0, (c ≠ –20).
d tiếp xúc với (E) khi và chỉ khi 
Với 
Với 
Vậy min (MN) =
Câu 21: Gọi z = a + bi (a, b ∊ ℝ) là số phức thỏa mãn điều kiện 
và có mô đun nhỏ nhất. Tính S = 7a + b?
A. 7
B. 0
C. 5
D. –12
Lời giải
Chọn A.
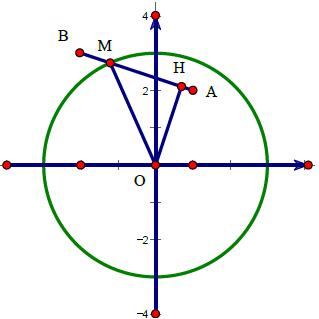
Gọi M (a; b) là điểm biểu diễn số phức z = a + bi.
A (1; 2) là điểm biểu diễn số phức (1 + 2i)
B (–2; 3) là điểm biểu diễn số phức (–2 + 3i), 
.